Einführung

Es ist an der Zeit in die Praxis einzusteigen. Wir ernten die Früchte unserer Arbeit und berechnen den fairen Preis europäischer Contingent Claims (im folgenden kurz Derivate genannt) im CRR-Modell. Zwei besonders wichtige Derivate sind die europäische Call- und Put-Option. Darüber hinaus sollen aber noch weitere Derivate betrachtet werden.

Europäische Call Option

Für die Auszahlung einer europäischen Call Option gilt \( C_T := (S_T - K)^+ \). Dabei nennen wir die Konstante \( K > 0 \) Strike. Wir wissen jetzt, dass für den fairen Preis \( \pi_{C} \) gilt:

\[ \pi_{C} = \frac{\mathbb{E}^{*}[C_T]}{(1 + r)^T} = \sum_{k = 0}^{T} {{T}\choose{k}} \cdot p_{u}^{k} \cdot p_{d}^{T-k} \cdot (S_0 \cdot (1 + r_{u})^{k} \cdot (1 + r_{d})^{T-k} - K)^+ \] \[ = \sum_{k = 0}^{T} {{T}\choose{k}} \cdot (\frac{r - r_{d}}{r_{u} - r_{d}})^{k} \cdot (\frac{r_{u} - r}{r_{u} - r_{d}})^{T-k} \cdot (S_0 \cdot (1 + r_{u})^{k} \cdot (1 + r_{d})^{T-k} - K)^+ \]

Europäische Put Option

Für die Auszahlung einer europäischen Put Option gilt \( P_T := (K - S_T)^+ \). Dabei nennen wir die Konstante \( K > 0 \) wiederum Strike. Der faire Preis \( \pi_{P} \) wird analog wie bei der Call Option berechnet. An dieser Stelle soll die Put-Call-Parität erwähnt werden, mit deren Hilfe man den Preis der Put Option berechnen kann. Die Put-Call-Parität ist

\[ C_T - P_T = (S_T - K)^+ - (K - S_T)^+ \]

\[ = S_T - K \]

Damit gilt für den Preis

\[ \pi_{P} = \frac{\mathbb{E}^{*}[P_T]}{(1 + r)^T} \]

\[ = \frac{\mathbb{E}^{*}[C_T - S_T + K]}{(1 + r)^T} \]

\[ = \pi_{C} - S_0 + \frac{K}{(1 + r)^T} \]

Europäische Optionen unter Variation von Parametern

Die folgenden Diagramme sollen dem Leser nur einen Eindruck davon verschaffen, wie sich der Preis einer klassischen europäischen Option verändert, wenn gewisse Parameter verändert werden (hier Strike, Laufzeit oder risikofreier Zins). Die Wahrheit ist, dass es deutlich komplizierter ist. Wir können hier nicht mal im Ansatz alle interessanten Fälle betrachten und diskutieren.

Für die nun folgenden Diagramme sind die Parameter wie folgt gewählt. Der Startpreis einer Aktie ist 100. Ein Up entspricht 0.1 und ein Down -0.1.

Das Diagramm zeigt einem das, was der Leser erwarten würde. Mit höherem Strike steigt der Preis einer Put Option und sinkt der Preis einer Call Option. Entspricht der Startpreis dem Strike, so ist der Preis der Call Option gleich der Preis der Put Option.

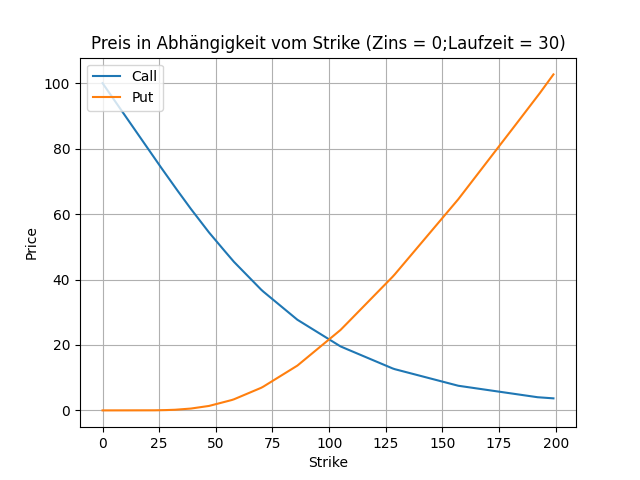
Diese Darstellung ist schon schwieriger zu interpretieren. Was auffällt ist, dass der Preis von Call- und Put-Option bei einem risikolosen Zins von 0 identisch sind. Die Put Option ist für negative Zinssätze sehr teuer. Der Abstand beider Kurven ist für einen Zinssatz größer 0 insgesamt deutlich kleiner.

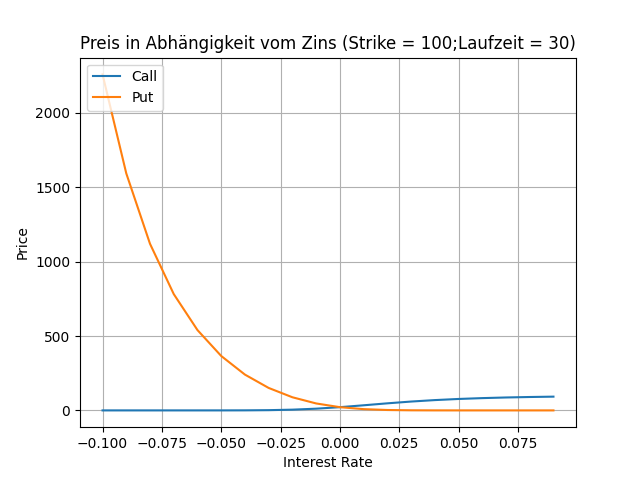
Bei den gegebenen Parametern sind die Kurven für den Preis einer Call- und Put-Option identisch. Der Preis nimmt mit steigender Laufzeit zu. Das kann man sich so erklären, dass die Wahrscheinlichkeit, dass die Option in den "Gewinnbereich" kommt, wenn ich eine längere Laufzeit habe. Ich will aber betonen, dass diese Kurve auch eine andere Form annehmen kann (und übrigens nicht identisch verlaufen muss). Wir werden die Auswirkung von Parameter-Variationen an einer anderen Stelle näher untersuchen.

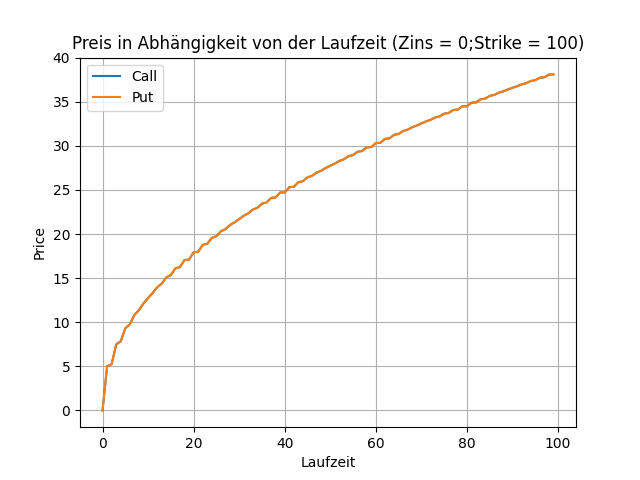
Binäre Option

Ich habe ein sehr spezielles Verhältnis zu binären Optionen und ich bin alt genug es zuzugeben. In der ersten Hälfte des letzten Jahrzehnts wurden binäre Optionen hoch beworben. Mein bester Freund und ich waren zarte 15 - 17 Jahre alt und hatte es faustdick hinter den Ohren. Über meinen Eltern haben wir ein Depot eröffnet und direkt (Gott sei Dank nur) 20 EUR verzockt. Ich werde diese Geschichte an einer anderen Gelegenheit nochmal aufrollen. Jetzt heißt es nicht kleckern, sondern klotzen.

Man könnte die Auszahlung einer binären Option ganz allgemein formulieren. Es sei \( E \) ein beliebiges Ereignis und \( a > 0 \). Dann definieren wir \( B_T := a \cdot \mathbb{1}_{A} \) als die Auszahlungsfunktion einer binären Option. Der Name hat offensichtlich etwas damit zu tun, dass der Investor nur zwei Auszahlungsmöglichkeiten hat. Er erhält einen fixen Betrag oder nichts. Das Pricing ist höchst unspektakulär. Es gilt

\[ \pi_{B} = \frac{\mathbb{E}^{*}[B_T]}{(1 + r)^T} = \frac{\mathbb{E}^{*}[a \cdot \mathbb{1}_{E}]}{(1 + r)^T} \]

\[ = a \cdot \frac{\mathbb{E}^{*}[\mathbb{1}_{E}]}{(1 + r)^T} = a \cdot \frac{\mathbb{P}^{*}[E]}{(1 + r)^T} \]

Üblicherweise beziehen sich binäre Optionen auf Ereignisse der Art \( E = \{ S_T \geq s \} \), \( E = \{ S_T \leq s \} \) oder \( E = \{ s_1 \leq S_T \leq s_2 \} \) mit \( s > 0 \) und \( 0 < s_1 < s_2 \). Man hat also die Möglichkeit auf steigende oder sinkende Kurse zu wetten. Oder aber man wettet darauf, dass ein Wertpapier innerhalb einer gewissen Schranke bleibt. Es gibt noch weitere Möglichkeiten binäre Optionen zu designen, aber dies seien die wichtigsten.

Forward Starting Call Option

Abschließend kommen wir nun zu einem etwas interessanterem Derivat. Eine Forward Starting Call Option hat die Auszahlung \( FC_T := (\frac{S_T}{S_{T_0}} - K)^+ \) für einen Strike \( K > 0 \) und einen Zeitpunkt \( 0 < T_0 < T \). Der unerfahrene Leser mag sich hier erstmal wundern, was es mit dieser Option auf sich haben könnte. Oder anders gefragt: Was ist denn hier konkret die Wette? Wir wollen Abhilfe verschaffen!

Im CRR-Modell gilt \( \frac{S_T}{S_{T_0}} = \frac{S_0 \cdot \prod_{t = 1}^{T} (1 + R_t) }{S_0 \cdot \prod_{t = 1}^{T_0} (1 + R_t) } = \prod_{t = T_0 + 1}^{T} (1 + R_t) \). Jetzt ist klarer worauf ein Investor wettet, wenn er so eine Option kauft, nämlich auf einen gewissen Kursanstieg eines Wertpapieres ab einen Zeitpunkt \( T_0 \). Was davor passiert, kann dem Investor praktisch egal sein. Damit ergibt sich für das Pricing

\[ \pi_{FC} := \frac{\mathbb{E}^{*}[FC_T]}{(1 + r)^T} \]

\[ = \sum_{k = 0}^{T_0} {{T_0}\choose{k}} \cdot p_{u}^{k} \cdot p_{d}^{T-k} \cdot ((1 + r_{u})^{k} \cdot (1 + r_{d})^{T_0 - k} - K)^+ \]

Ausblick

Die oben beschriebenen Terme lassen sich ohne Probleme implementieren. Ich empfehle jeden Leser die oberen Ausdrücke in Code (gerne auch Excel) zu gießen und mit den Parametern zu spielen.

Das Pricing im CRR-Modell ist für die oberen Derivate einigermaßen simpel. Interessant ist es jedoch sich exotischere Derivate anzuschauen, für die das Pricing mit etwas mehr Aufwand verbunden ist. Uns wird auch interessieren welche Form von Derivaten nicht mit unserer Methode sinnvoll gepreist werden können.

Ich möchte aber betonen, dass der Leser jetzt schon eine gute Handvoll gängige Derivate kennt. Mit dem oben beschriebenen Inhalt lässt sich schon eine ganze Menge anstellen. Wenn wir im nächsten Teil mit exotischen Derivaten und den Grenzen unserer Methode auseinandergesetzt haben, wollen wir mit konkreten Marktdaten arbeiten.